 terabo.net
terabo.net 人生ラボラボ
Fewest moves challenge と God’s number

先日、2015年10月11日にアメリカ合衆国カリフォルニア州アーバインで開催された Irvine Fall 2015 で Tim Wong 氏が Fewest moves challenge (FMC: 最少手数競技) で 19手 という大記録を達成し世界記録を更新しました。
Tim Wong (from USA) just got the 3x3x3 FMC single WR (19) at Irvine Fall http://t.co/2bucmuJgPR
— Cubecomps (@cubecomps) 2015, 10月 11これまで Fewest moves の世界記録は 20手 で、保持者は
- Rami Sbahi 氏 (2015年、Michigan 2015) ( 解法解説ビデオ)
- 岡山友昭 氏 (2012年、Czech Open 2012) ( 解法紹介ビデオ)
の2人でした。
Contents
はじめに (God’s number)
3x3x3キューブ (ルービックキューブ) の God’s number と呼ばれる数字が存在します。
God’s number が 20 であるということは、つまりひとことで言うと、
「どのようにスクランブルされた3x3x3キューブでも必ず20手†1以内で完成できる」
ということです。
†1 注釈: ここで言う20手とは HTM (Half Turn Metric) すなわち90度回転・180度回転をともに1手と数える世界での話です。本記事ではHTMのみを考えます。 なお、QTM (Quarter Turn Metric) での God’s number が 26 であることが2014年8月に証明されたのですが (結構最近!)、その話は気が向いたらいつかしたいと思います。 今回はHTMのみを考えます。
Wong 氏の19手という記録は公式大会では初めて God’s number を上回ったことから、 キューバーの間では「神を超えた (sub God)」というジョークがかわされています。
神を超えた男 Tim Wong
— Kotaro Terada (@kotarotrd) 2015, 10月 11ついに神を超える者が現れたか…
— Morooka (@morooka_cube) 2015, 10月 12さて、公式大会で God’s number を上回る数字を出したということで、次のような疑問が生じてきます。
- God’s number is 20 だから、『絶対に』WRを出せない (すなわち、20手未満の解答が存在しない) スクランブルに遭遇してしまう可能性はないのか?
- 『絶対に』WRを更新できない (すなわち、19手未満の解答が存在しない) スクランブルに遭遇してしまう可能性はどうなのか?
- FMCで出題されたスクランブルからの20手以内の完成手順は一体何通りぐらいあるのか?
- FMCで出題されたスクランブルからの19手以内の完成手順は一体何通りぐらいあるのか?
本記事はこの4つの質問に答えていこうと思います。 先に答えを書いてしまうと、
- そのような確率は 限りなく0に近い (ジャンボ宝くじで1等当選よりずっとずっと低い確率)
- 残念ながらこれは起こりうる確率があって、約3%
- ランダム状態からの20手以内の完成手順は平均して 約1000通り (ただしこれはかなり大雑把な数字、詳細は後述)
- ランダム状態からの19手以内の完成手順は平均して 約80通り (ただしこれも結構アバウトな数字、詳細は後述)
本記事の残りのパートではその根拠を書いていきます。 時間がある方はよかったらお付き合いください。 上で書いた質問は、単純に私が疑問に思ったことでもあるので簡単に調査してみた、という記事でもあります。 あと、あらかじめ書いておきますが、本記事はFMCのWR更新を取っ掛かりとしてキューブのアルゴリズム的アプローチから見た考察を書いただけなので、 これを読んでもFMC技術の向上にはつながりません。
本記事は「2章 cube20.org プロジェクトの功績」、「3章 冒頭の質問に答える」、「4章 まとめ」と続きます。 手っ取り早く読み終えたい方は「4章 まとめ」へ、 理論的なバックグラウンドはどうでもいいので答えの理由を知りたい方は「3章 冒頭の質問に答える」へジャンプしてください。 詳しく知りたい方は次の「2章 cube20.org プロジェクトの功績」からお読みください。
cube20.org プロジェクトの功績
前提知識として、3x3x3キューブの理論的な話をします。
cube20.org というプロジェクトページがあります。 これは God’s number is 20 であることを証明した Tomas Rokicki らの研究チームのプロジェクトページです。 具体的に証明の詳細や God’s number の歴史がまとめられています。
God’s number が 20手であることを言い換えると次のようになります。
- 任意の状態の3x3x3キューブは完成状態まで高々20手で到達可能である
(i.e., 任意状態から完成までの最短手順の手数の上限値は20である)。 - 完成状態まで最短でも少なくとも20手を要するような3x3x3キューブの状態が存在する
(i.e., 任意状態から完成までの最短手順の手数の下限値は20である)。
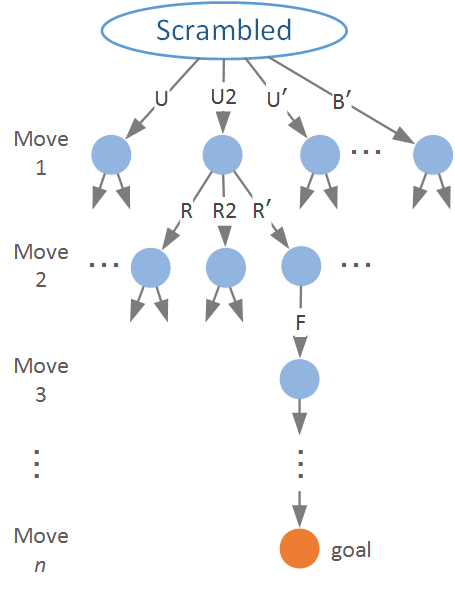
今後の議論において定式化として、 3x3x3キューブの色の配置を状態ノードとして扱い、探索には search tree を用いて考えます。 この辺は詳しくは過去に書いた記事をご覧ください。
3x3x3キューブの取り得る全パターン数
これは知っている方は多いとおもいますが、
3x3x3キューブの完成状態から到達可能な全パターン数 (状態数) は、
はたむらさんのブログ記事で説明されている
ように、計算すると
$(12! \cdot 8! \cdot 2^{11} \cdot 3^{7})/2 = 43,252,003,274,489,856,000$
(約4300京) です (Wolfram|Alpha 計算結果)。
最短手順手数の下限値
まず、下限値を計算します。 下限値は search tree の状態ノードと3x3x3キューブの全パターン数を比較することで比較的簡単な計算で求めることができます。
簡易的に計算する
ある状態から単純に各6面を3通りに合計18通りの回し方を考えると、
完成状態から $n$ 手回したとき $18^n$ 個 の状態が展開されます。全状態数はそこまでの総和です。
このとき、
${\displaystyle \sum_{n=0}^{15} 18^n} = 7,143,501,829,211,426,575$ (Wolfram|Alpha 計算結果)
${\displaystyle \sum_{n=0}^{16} 18^n} = 128,583,032,925,805,678,351$ (Wolfram|Alpha 計算結果)
であるから、
${\displaystyle \sum_{n=0}^{15} 18^n \lt 全パターン数 \lt \sum_{n=0}^{16} 18^n}$
です。
15手までを考えた search tree の各状態ノードにキューブのパターンを1対1に割り当てたとしても
全パターンを割り当て切れないため、鳩の巣原理より 下限値は16手 であることは自明です。
数式が単純なので、Wolfram|Alpha で計算させましたが、以下のPythonスクリプト (メイン部分の行のみ表示) でも計算できます。
すこし賢く計算する
しかし、同じ面を連続して回すことは状態数が重複してしまい冗長です。
例えば、1手目でUを回して2手目でU2を回すと完成状態からU’された状態になるがこれはすでに1手目でU’して展開された状態と等しいです。
そこで、完成状態から $n$ 手回したとき $18 \cdot 15^{(n-1)}$ 個 の状態が展開されることを考えればよいです。全状態数はそこまでの総和です。
このとき、
${\displaystyle 1 + \sum_{n=1}^{16} 18 \cdot 15^{(n-1)}} = 8,445,096,457,345,145,089$ (Wolfram|Alpha 計算結果)
${\displaystyle 1 + \sum_{n=1}^{17} 18 \cdot 15^{(n-1)}} = 126,676,446,860,177,176,339$ (Wolfram|Alpha 計算結果)
であるから、
${\displaystyle 1 + \sum_{n=1}^{16} 18 \cdot 15^{(n-1)} \lt 全パターン数 \lt 1 + \sum_{n=1}^{17} 18 \cdot 15^{(n-1)}}$
です。
同様にして、下限値は17手 であることがわかります。
これも Wolfram|Alpha で計算しました。以下のPythonスクリプトでも計算できます。
もっと賢く計算する (canonical sequences)
さらに状態の冗長性排除を試みます。 直前の2手で対面の回転が適用された場合、次の回転は隣接面のみ考えれば十分です。 例えば、1手目がU、2手目がD2の場合、3手目においてU面かD面をどのように回しても2手目までの状態と必ず重複しますので冗長です。 これを考慮するために、さっきの制限に加え、D→U、B→F、L→R と続く動きを排除します。 これで目的が達成されます。 これを計算する数式が考えつかなったので、Pythonスクリプトで計算します。
ここで、$n$ 手回したときに展開される合計ノード数を $\sigma (n)$ と置くと、
$\sigma (17) = 19,973,266,111,335,481,264$
$\sigma (18) = 266,612,528,076,798,235,312$
と計算されます。
$\sigma (17) \lt 全パターン数 \lt \sigma (18)$
であるから、同様にして、下限値は18手とわかります。
なお、この計算によって展開される手順列のことを
God’s number is 20 の論文では
canonical sequences という用語で定義されています。
アルゴリズムを応用して厳密に計算すると……
と、ここまでは単純に search tree の状態数と3x3x3キューブの全パターン数の比較計算によって下限値が計算されましたが、 1995年、Michael Reid によって下限値が20であることが示されました。 これは superflip と呼ばれる状態 (コーナーは完全に揃っていてエッジは位置は正しいがすべてフリップしている状態) がどうやら難しいだろうという推測をして、 Kociemba’s algorithm を応用することで superflip を解く手順を徹底的に調べたら、 superflip を解くには 少なくとも20手必要であることがわかった ということです。
- Cube Lovers: superflip
- Cube Lovers: more on superflip
- Cube Lovers: superflip requires 20 face turns
- Cube Lovers: Re: superflip requires 20 face turns
- Cube Lovers: superflip in 20f
最短手順手数の上限値
上限値を計算することは、下限値の計算と比べて難しい課題でした。
なぜなら下限値は約4300京通りの全パターンの中から20手必ず要するような状態 (例えば superflip) を1つでも見つければよかったのに対し、
上限値は約4300京通りの全パターンが$X$手以内で必ず解けるような$X$を見つける必要があるからです。
上限値の計算は、アルゴリズムの歴史とコンピュータハードウェアの進化の歴史で語れます。
歴史を長々と書いてもしょうがないので、ポイントだけ書きます。
さっきも出てきましたが Kociemba’s two-phase algorithm という、
問題を2つのフェーズ (2つのサブ問題) に分割して解くアルゴリズムが優秀でした。
アルゴリズムの詳細は Kociemba氏のwebサイト に書いてあると思います。
さっきもリンク貼ったけど 以前書いた記事 にもいろいろ書いたような気がします。
さて、ここからがポイントなのですが、 さっき書いたように1995年に下限値が20手であることが示されました。 よって、ある状態から完成状態までへの最短手数 (最適解) が何手であろうと、20手以内に完成できることだけが示せれば良いのです。 下限値が20であることが確定している以上、上限値は20を下回ることはありえないからです。
実は Korf’s algorithm という IDA* 探索アルゴリズム をベースとした任意状態からの最適解 (最短手順) を計算する アルゴリズムが存在するのですが、このアルゴリズムで最適解を求めるには 多くの時間とメモリを消費します。 例えば、ランダム状態のキューブを1つ与えられてその最適解を計算する、といった用途には耐えられるのですが、 全4300京通りのパターンを調べあげるという用途ではとてもじゃないが実行不可能だということが予想されています。 God’s number is 20 の論文 では、 このアルゴリズムを使用して全パターンの最適解を求めるには 70億CPU年†2を要すると述べられています。
†2 注釈: X CPU年 (or CPU時間) とは、もしシングルマシン・シングルCPU・シングルプロセス・シングルスレッドで実行した場合に、 完了するまでにX年 (or 時間) を要するという意味です。
そこで、God’s number is 20 プロジェクトで Tomas Rokicki らは、 Kociemba’s two-phase algorithm を用いて計算しました。 Kociemba’s algorithm は Korf’s algorithm と異なり一般に最適解は求められないものの、 Korf’s algorithm と比較して桁外れに高速なアルゴリズムです。 今回は最適解を求めることができなくても20手以内の解法を見つければ良いため、 Kociemba’s algorithm が最適でした。 Kociemba’s algorithm は最適解は求められないものの20手以内ぐらいの解答であれば高速で計算できることがわかっています。 (ちなみに、WCA公式スクランブラの TNoodle も Kociemba’s algorithm が用いられています)。 Tomas Rokicki らは、詳細は省略しますが全4300京パターンを対称性に注目し小さなグループに分割し、 Google社が所有する巨大な分散サーバコンピュータで計算実験しました。 2010年7月、全4300京パターンの全てについて20手以内の解答を見つけました。 プログラムの実行には35CPU時間を要したと報告されています。
最適解手順の手数の分布
2010年の Tomas Rokicki らの仕事により上限値20と下限値20が一致し確定したため、 20という数字は今後永遠に更新されなくなりました。 それが God’s number is 20 と呼ばれる理由です。
Tomas Rokicki らの cube20.org プロジェクトは、 全4300京のパターンに20手以内の解答が存在することを示すと同時に、 最適解の手数の分布を公開しています。 ここでは、それを引用します。
前述のように全4300京パターンの最適解を計算することは現在の技術では不可能ですが、 最適解手順の手数が0手から15手までのパターンは厳密に計算されています。
| 完成までの最短手数 | パターン数 (状態数) |
|---|---|
| 0 (完成状態) | 1 |
| 1 | 18 |
| 2 | 243 |
| 3 | 3,240 |
| 4 | 43,239 |
| 5 | 574,908 |
| 6 | 7,618,438 |
| 7 | 100,803,036 |
| 8 | 1,332,343,288 |
| 9 | 17,596,479,795 |
| 10 | 232,248,063,316 |
| 11 | 3,063,288,809,012 |
| 12 | 40,374,425,656,248 |
| 13 | 531,653,418,284,628 |
| 14 | 6,989,320,578,825,358 |
| 15 | 91,365,146,187,124,313 |
出典: T. Rokicki, H. Kociemba, M. Davidson, and J. Dethridge, “The diameter of the rubik’s cube group is twenty,” SIAM J. Discrete Math., vol. 27, no. 2, pp. 1082–1105, 2013. [pdf]
最適解手順の手数が16手以上のパターン数は厳密に計算できないものの、 本研究グループは推測値を公開しています。
| 完成までの最短手数 | パターン数 (状態数) |
|---|---|
| 16 | 約 1,100,000,000,000,000,000 |
| 17 | 約 12,000,000,000,000,000,000 |
| 18 | 約 29,000,000,000,000,000,000 |
| 19 | 約 1,500,000,000,000,000,000 |
| 20 | 約 300,000,000 |
| 20 以上 | 0 |
出典: T. Rokicki, H. Kociemba, M. Davidson, and J. Dethridge, “The diameter of the rubik’s cube group is twenty,” SIAM J. Discrete Math., vol. 27, no. 2, pp. 1082–1105, 2013. [pdf]
なお、最適解が20手であると予想されている 約300,000,000通りのうち、 93,659,370通りは19手以下の解答を持たないことが確かめられています (記事執筆時点)。
冒頭の質問に答える
前置きが長くなりましたが、 以上の知識をベースとしてここで本記事の冒頭に掲げた質問に回答していきたいと思います。
1つ目の質問の答え
質問は
God’s number is 20 だから、『絶対に』WRを出せない (すなわち、20手未満の解答が存在しない) スクランブルに遭遇してしまう可能性はないのか?
でした。
まず、「全パターンの出現する確率は一意である」という仮定を置きます。 通常のスクランブルプログラム (公式スクランブル生成プログラム TNoodle を含む) はランダム状態を生成してスクランブルを計算するため、 この仮定はごく自然です。
その上で、これに回答するためには、 上で引用した表で最短手順が20手であるような状態数が全状態数 (約4300京) に占める割合を計算すれば良いです。
$300,000,000 / 43,252,003,274,489,856,000 \approx 7 \times 10^{-12} = 0.000000000007$
と計算されます。
パーセントに直すと、約0.0000000007% です。
日本語で書くと、約1000億分の1 です。
これは限りなく0に近い確率でまず出現しないと言えるでしょう。
ジャンボ宝くじ1等の当選確実は1000万分の1らしい ので、『絶対に』世界記録を出せないスクランブルに遭遇する確率はそれよりもずっとずっと低い確率ということがわかります。
2つ目の質問の答え
質問は
じゃあ、『絶対に』WRを更新できない (すなわち、19手未満の解答が存在しない) スクランブルに遭遇してしまう可能性はどうなのか?
でした。
質問の内容は1つ目とほぼ同じですね。
最適解が19手以上の状態数を全パターン数で割ります。計算すると、
$(1,500,000,000,000,000,000 + 300,000,000) / 43,252,003,274,489,856,000 \approx 0.0347 = 3.47\%$
です。約3% らしいです。
これは十分起こり得る確率であると言えます。
1つ目と2つ目の疑問に関連したことで、
表からすぐわかることですが、与えられたランダム状態のキューブの最適解が$X$手である確率を$P(X)$で表すことにすると、
P(18) > P(17) >> P(19) > P(16) >> (ここまでで99.8%) >> P(15) > P(14) > P(13) > P(12) > P(11) > P(10) >
P(9) > P(8) > P(20) > P(7) > P(6) > P(5) > P(4) > P(3) > P(2) > P(1) > P(0)
です。
今、あなたがスクランブルしたキューブ (スクランブルジェネレータを用いた場合でも十分に長いランダム回転を与えた場合でも)、
その状態を最短で解く手順の手数はほぼ確実に18手か17手、運が良ければ19手か16手、かなり運が良ければ15手でしょう。
ちなみに、今回Wong氏がWR樹立したスクランブルの最適解は
17手だそうです。
3つ目の質問の答え
質問は
FMCで出題されたスクランブルからの20手以内の完成手順は一体何通りぐらいあるのか?
でした。
これは答えるのが難しい質問です。 なぜなら最適解の完全な解が計算されていない (手数が16手以上のとき) こと、 つまり search tree 上に各状態ノードがどのような分布で存在しているかがわからないからです。
ここで、大雑把な仮定を置きます。
「すべてのキューブ状態は search tree 上の状態ノードに均一に分布している」とします。
そのよう仮定の上、あるキューブの状態パターンが平均して、完成状態から20手まで展開した search tree 上の何個の状態ノードに対応しているか計算します。
$n$手まで展開した search tree のノード数は、この記事の中盤で計算した canonical sequences の数のことで、
$\sigma (20) = 47,505,455,028,489,778,073,776$
であるから、
$47,505,455,028,489,778,073,776 / 43,252,003,274,489,856,000 \approx 1098$
と計算されて、search tree 上に同一のキューブ状態を表す状態ノードが平均して約1000個存在することになります。
これは言い換えると、ある状態から完成手順に至るまでの20手以内の異なる手順は約1000種類ある (ただし平均値) ということです。
平均なので気をつけなければいけないことは、 例えば、ある状態からの完成手順が1通りしかないとしても、別のある状態からの完成手順が1999通りあれば、平均は1000通りです。 よって、1000通りという数字は本当に意味が数値なのかどうかはよくわかりません。
4つ目の質問の答え
質問は
FMCで出題されたスクランブルからの19手以内の完成手順は一体何通りぐらいあるのか?
でした。
3つ目の質問とほぼ同じです。計算方法も同じです。
$\sigma (19) = 3,558,869,126,925,617,486,512$
であるから、
$3,558,869,126,925,617,486,512 / 43,252,003,274,489,856,000 \approx 82$
と計算されます。
言い換えると、ある状態から完成手順に至るまでの19手以内の異なる手順は約80種類ある (ただし平均値) ということです。
これも、例えば、 既に最短手順が20手であるとわかっているような状態 (superflipに代表されるような約300,000,000パターンあると推測されている状態) から19手以内の完成手順は0通りであることは明らかですので、 あくまでも平均値であるということに気をつける必要があります。 回答3と同様にナンセンスな数値かもしれません。
まとめ
結論を書きます。
結局、この記事を通して何がわかったのかまとめます。
- ランダム状態のキューブに対して、ほぼ確実に (ジャンボ宝くじ1等が外れるよりとても高い確率で) 19手以内で解く手順が存在し、かなり高い確率 (約97%) で18手以内で解く手順が存在する。
- ランダム状態のキューブに対して、20手以内で解く手順は平均で約1000通り、19手以内で解く手順は平均で約80通り存在する。
2つ目の「20手以内で解く手順は平均で約1000通り、19手以内で解く手順は平均で約80通り存在する」という部分†4、 この数字を大きい値見るか小さいと見るかは人それぞれ感じ方があると思います。
†4 注釈: ちなみに、この内の1手順はスクランブルの逆手順である可能性が高いです。 WCAデータベースに登録されているこれまで実施されたFMC競技の全634スクランブルの手数の分布は、 16手 1回、17手 19回、18手 69回、19手 218回、20手 264回、21手 63回、です (2015年10月15日時点)。 スクランブル手順は20手以下であることがほとんどです。
今回は、FMCの世界記録更新と God’s number をテーマに取り上げましたが、 私などをはじめとするFMC未熟練者がまず踏み出せそうな最初の目標 sub30 も本記事で説明した計算式を用いて同じように考えることができて、 「ランダム状態のキューブからの29手以下の完成手順は約15兆通り存在する」と計算することができます。 1000通りとか80通りなんかというレベルではありません (それだけ分母となる手順数が増えるのでこの比較自体にはあまり意味がないと思いますが)。
私はこれらの数値を見て、直感的に意外と多いんだな、って思いました。 もちろんこれらの数値を満たすような手順のほとんどは人間が理解できるアルゴリズムから大きくかけ離れたものでしょう。 しかし、個人的には望みを感じます。
現時点ではまだまだキューブの完全解析 (全パターンの最適解を知ること) へは遠い道のりに見えますが、 おそらく、完全解析されるのも時間の問題でしょう。 それはそれでコンピュータサイエンスにいる側の人間としては興味深いテーマなのですが、 スピードキュービングにいる側の人間としては人間が God’s number にどこまで迫れるかというところに非常に深いおもしろさがあると思います。
神†5はすべてにおいて人間を超越します。 人間は神を追い越すことはできません。 いずれ3x3x3キューブは完全解析されてコンピュータは神になるでしょう。 そこに人間がどこまで迫れるかというところに頭脳を使うマインドスポーツのおもしろさがあります。
†5 注釈: ここでの神とは宗教的な神という意味ではなく、最適化問題の神様、つまりどんな状況でも常に最適解を一瞬で見つける存在、という意味です。 というか、冒頭から書いている God もそういう意味での神なんで、今更ですが。
もちろん人間は神様と違い全パターンを調べるというのは不可能であるため、 アルゴリズムにしたがって解法を見つけるしかありません。 問題が大きすぎるから適度な大きさの問題に絞り込むことで 人間の頭の回転速度で解けるように問題を変換します (FMCの場合これの主たるものは block building です)。 $18^{20}$ ~ $18^{30}$ という神様しか扱えない膨大なサイズの探索空間からアルゴリズムを用いることで人間が1時間で扱える問題のサイズへ変換します。
アルゴリズムというのは言い換えると制限を与えることです。 制限を与えることで問題を解きやすくします。 問題をごく一部しか考えないということは、ほとんどの (ひょっとしたら全部の) 最適解・準最適解を切り落としているということが言えます。 これは、見方を変えると、神から見たら人間はアルゴリズムという拘束具をまとったうえで、 問題を解いているということです。 スピードキュービングの世界において、単純に1つのアルゴリズム (CFOP でも Roux でも ZZ でも block building でも) を用いたときの局所最適解は、全体最適解からかけ離れたものになるのが普通です。
「アルゴリズムは諸刃の剣」です。 アルゴリズムは答えを見つけるための優秀なガイドであり、また解答を制限する拘束具でもある一面を見せます。 人間はアルゴリズムがないと答えを見つけられません。 しかしそのアルゴリズムが同時に最適解を見つける障害にもなっているという、もどかしい世界です。
FMCを勝するキーポイントは、拘束具としてのアルゴリズムを打ち壊すことだと考えています。 もちろん純粋にアルゴリズムに従って最適解・準最適解を見つけられたらそんなおいしい話はありません (LL skip なんかはこれに若干含まれると思いますが)。 アルゴリズムの殻を打ち破ること、 それは小手先の技術 (pre-move やコミュテータインサート等) を含んだ様々なアルゴリズムを知っていることであったり、 競技時間内にいろいろなアルゴリズムを試せるような能力であったり、 またときには純粋な運であったりします。
実際今回のスクランブルは逆スクランブルで F2L-1 まで9手という好スクランブルでありました。 そういう意味ではラッキーなスクランブルではあり運がよかったと言えると思います†6。 しかし、Wong 氏のそこから終盤にかけて19手でまとめ上げる技術力には感服です。
†6 注釈: Wong 氏がWR出したスクランブルと解答です。
参考: [WR] Tim Wong FMC 19 moves,
and InsertionFinder
Scramble: R2 B' U2 L2 B R2 B2 D2 R2 B R' D2 B' D F D L B2 D' U2 Inverse scramble: U2 D B2 L' D' F' D' B D2 R B' R2 D2 B2 R2 B' L2 U2 B R2 F2L-1: R2 F L2 B' R' F2 B L B2 L3C: R D' F D2 F' D R' D' Skelton: R2 F L2 B' R' F2 B L B2 R D' F D2 F' D R' D' [@1] Insert at @1: D R D' L' D R' D' L ---- Solution for inverse: R2 F L2 B' R' F2 B L B2 R D' F D2 F' L' D R' D' L Final solution: L' D R D' L F D2 F' D R' B2 L' B' F2 R B L2 F' R2 (19 moves)
試行回数(≒運) と日々の練習により積み重ねられ熟練した技術と勘によって達成されたこの世界新記録は、 偉大な大記録であったと言うしかありません。
Congratulations, Tim Wong!
そしてWR奪還の期待を願って、この記事を終えたいと思います。
以上、長々と書きましたが、お読みいただきありがとうございました。
終わりだよ~